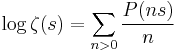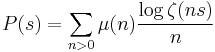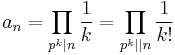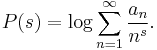Prime zeta function
In mathematics, the Prime zeta function is an analogue of the Riemann zeta function, studied by Glaisher (1891). It is defined as the following infinite series, which converges for 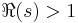 :
:
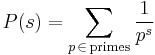 .
.
The Euler product for the Riemann zeta function ζ(s) implies that
which by Möbius inversion gives
When s goes to 1, we have 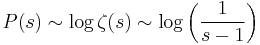 . This is used in the definition of Dirichlet density.
. This is used in the definition of Dirichlet density.
This gives the continuation of P(s) to 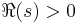 , with an infinite number of logarithmic singularities at points where ns is a pole or zero of ζ(s). The line
, with an infinite number of logarithmic singularities at points where ns is a pole or zero of ζ(s). The line 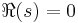 is a natural boundary as the singularities cluster near all points of this line.
is a natural boundary as the singularities cluster near all points of this line.
If we define a sequence
then
(Exponentiation shows that this is equivalent to Lemma 2.7 by Li.)
References
- Merrifield, C. W. (1881). "The Sums of the Series of Reciprocals of the Prime Numbers and of Their Powers". Proc. Roy. Soc. London 33: 4–10. doi:10.1098/rspl.1881.0063. JSTOR 113877.
- Fröberg, Carl-Erik (1968). "On the prime zeta function". Nordisk Tidskr. Informationsbehandling (BIT) 8 (3): 187–202. doi:10.1007/BF01933420. MR0236123.
- Glaisher, J. W. L. (1891). "On the Sums of Inverse Powers of the Prime Numbers". Quart. J. Math. 25: 347–362.
- Mathar, Richard J. (2008). "Twenty digits of some integrals of the prime zeta function". arXiv:0811.4739. Bibcode 2008arXiv0811.4739M.
- Li, Ji (2008). "Prime graphs and exponential composition of species". J. Combin. Theory A 115: 1374—1401. doi:10.1016/j.jcta.2008.02.008. MR2455584.
- Mathar, Richard J. (2010). "Table of Dirichlet L-series and prime zeta modulo functions for small moduli". arXiv:1008.2547. Bibcode 2010arXiv1008.2547M.